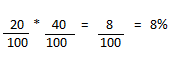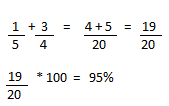Juliana Jenny Kolb
Home > Concursos > Questões de Concursos > Conhecimentos Gerais > Matemática e Raciocínio Lógico
Materiais de Estudo disponíveis
| Apostila on-line |  |
Respostas dos Exercícios – Porcentagem
Resolução nr. 1: A fração correspondente ao complemento de 20% de 40% é:
O todo é 100%, o complemento seria: 100% – 8% = 92%
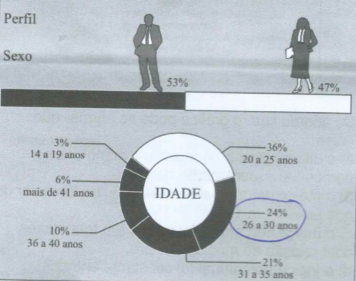
Resolução nr. 2: Levantamento realizado por um varejista mostra a distribuição porcentual, por sexo e faixa etária, dos compradores do produto XIS em determinado período.
Sabendo-se que, nesse período, a diferença entre o número de homens e o de mulheres que compraram esse produto foi igual a 48, pode-se afirmar que o número de pessoas de 26 a 30 anos que compraram o produto XIS, nesse período, foi
Equação 1:
Do enunciado, temos:
H – M = 48
Equação 2:
Utilizando o conceito de que parte está para o todo:
Montando o sistema:
Equação 1: H – M = 48
Equação 2: 47 H = 53 M
M = 376
H = 424
Faixa de 26-30 anos = 24%
24/100 * 800(total de pessoas) = 192
Resolução nr. 3: Mauro pagou R$ 360,00 por um produto já incluso 20% de desconto sobre o valor à vista do mesmo. Se o desconto fosse de 10% sobre o valor à vista do produto, então Mauro pagaria pelo produto:
x (100% – 20%) = 360
x * 80% = 360
80 x /100 = 360
x = 450 (preço da etiqueta)
10% de desconto:
y = 10/100 * 450
y = 45 (10% desconto)
Valor com desconto:
450 – 45 = 405,00
Resolução nr. 4: Um comerciante pagou R$ 560,00 por um produto e o vendeu com um lucro de 30%. Aplicou por 2 meses o valor que obteve pela venda desse produto a uma taxa mensal de juros simples de 5%. Então, o valor que recebeu de juros, nesses dois meses foi de:
C = 560,00 + 30%
C = 560 + (30/100 * 560)
C = 728
n = 2
i = 5% = 5/100
Aplicando a fórmula: J = C * i * n
J = 728 * 5/100 * 2
J = 72,8
Ver: Juros Simples e Compostos (+)
Resolução nr. 5: Joaquina comprou os seguintes produtos numa loja: uma geladeira de R$ 1.240,00, um fogão de R$ 750,00 e um micro-ondas de R$ 450,00, pagou os três produtos em 10 vezes sem juros, porém na sexta prestação atrasou o pagamento. Sabendo que a multa por atraso foi de 15% sobre o preço da parcela, o valor que Joaquina pagou pela prestação foi de:
Total da compra = 2.440,00
Cada parcela = 2.440 / 10 = 244
15% de multa na parcela = 15/100 * 244 = 36,6
Total pago na parcela = 244 + 36,6 = 280,60
Resolução nr. 6: 30% de 40% de 150 é igual a:
40/100 * 150 = 60
30/100 * 60 = 18
Resolução nr. 7: Maria gastou 3/8 da quantia que possuía com vestuário e 1/2 do restante com alimentos. A percentagem que representa a quantia que sobrou para Maria é igual a:
Resolução nr. 8: Marcos estava sem dinheiro, então foi ao banco e sacou certa quantia para pagar uma dívida cujo valor corresponde a 30% da quantia que sacou. Com 40% do que restou comprou um produto numa loja, restando-lhe ainda R$ 1.050,00. A quantia que Marcos sacou é igual a:
Saque => 70 % + 30 %
Sabemos que destes 70 %, que vamos chamar de x, 40% comprou em produtos e sobrou 1.050, então
x =( 40/100 x )+ 1050
x = 1750 => correspondendo a 70% do saque
Temos:
1750 = 70%
y = 30%
y = 750 => correspondendo a 30% do saque
Saque = 1750 + 750
Saque = 2500
Resolução nr. 9: A Farmácia do Sr. Antunes costuma comprar medicamentos sempre do mesmo distribuidor e revendê-los à população com lucro de 30%. Na última semana, o distribuidor aumentou seus preços em 10%, porém o seu Antunes decidiu não repassar esse aumento aos seus clientes. Portanto, o lucro do Sr. Antunes diminuiu para aproximadamente:
Para dar continuidade, atribua ao medicamento um valor, por exemplo: 100
Antes do aumento:
Aplicando a fórmula: Valor Inicial * (100% + i) = Valor Final
100 * (100% + 30%) = VF
VF = 130 (lucro inicial)
Aumento do Distribuidor:
Aplicando a fórmula: Valor Inicial * (100% + i) = Valor Final
100 * (100% + 10%) = VF
VF = 110
Sr. Antunes continuará vendo por 130,00, mas o custo aumento para 110,00, desta forma, o lucro será de somente 20,00.
Se:
110 = 100%
20 = x
x = 18,18%
Resolução nr. 10: Uma fração pode representar uma porcentagem. Exemplo: 1/2 equivale a 50%. Então 1/5+3/4 equivale a :
Resolução nr. 11: Ana comprou um produto e pagou R$ 45,00, já incluso um desconto de 10%. O valor de dois produtos, sem desconto, idênticos ao que Ana comprou, é de:
Aplicando a fórmula: Valor Inicial * (100% – i) = Valor Final
VI * (100% – 10%) = 45
VI * (90/100) = 45
VI = 50
Dois produtos => 50 * 2 = 100,00
Resolução nr. 12: João gastou 3/8 de seu salário com alimentação. A porcentagem do salário de João que ainda sobrou foi de:
3/8 de 100, ou seja
3/8 * 100 = 37, 5% do salário
100% – 37,5% = 62,5%
Resolução nr. 13: Sabendo-se que uma pessoa tem 80% do valor de seu aluguel e faltam 400 reais para conseguir saldar este pagamento. Pode-se afirmar que:
80% = x
20% = 400
Então,
20 x = 80 * 400
x = 1600 (corresponde a 80%)
Aluguel = 80% + 20%
Aluguel = 1600 + 400
Aluguel = 2000
Resolução nr. 14: Comprei uma calça e obtive um desconto de R$ 20,00, equivalente a 25 % sobre o preço da mesma. O valor que paguei na calça, considerando o desconto, foi de
x * 25/100 = 20
x = 80 (valor da calça sem desconto)
80 – 20 (desconto) = 60
Resolução nr. 15: A fração 4/20 é equivalente a:
A forma mais fácil de resolver é observar as respostas, que estão em %, ou seja, “/100”
Então, temos que transformar o “/20” em “/100” e, para isso, multiplicamos tanto o numerador quanto o denominador por 5.
4 * 5 / 20 * 5 = 20/100
Resolução nr. 16: Lívia comprou um produto para revender e pagou R$ 136,00 obtendo 20% de desconto no preço à vista do produto. O lucro de Lívia ao vender o produto ao vender o produto com 25% de acréscimo em relação ao preço à vista foi de:
Aplicando a fórmula: Valor Inicial * (100% – i) = Valor Final
VI * (100% – 20%) = 136
VI = (80/100) = 136
VI = 170
Aplicando a fórmula: Valor Inicial * (100% + i) = Valor Final
170 * (125/100) = VF
VF = 212,50
Lucro = 212,50 – 136 = 76,50