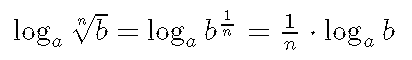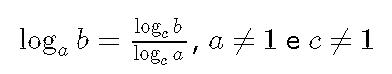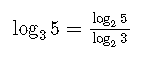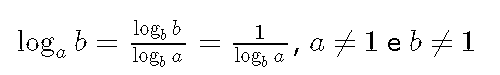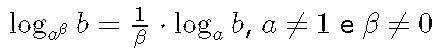Compartilhando | Logaritmos

Juliana Jenny Kolb

Home > Concursos > Questões de Concursos > Conhecimentos Gerais > Matemática e Raciocínio Lógico

Logaritmos

Sendo a e b números reais positivos, chama-se logaritmo de b na base a, o expoente em que a deve ser elevado de modo que a potência obtida de base a seja igual a b.

log_ab = x, logo

a^x=b

Com a>0, a≠1 e b>0

Assim, o logaritmo nada mais é que um expoente. Dizemos que “a” é a base do logaritmo, “b” é o logaritmando e “x” é o logaritmo.

Exemplo:

log₂ 16 = 4, pois 2⁴ = 16.

Definições

I) O logaritmo cujo o logaritmando é igual a 1 e a base é qualquer, é igual a zero:

log_a 1 = 0, pois a⁰ = 1

II) O logaritmo cujo a base e o logaritmando são iguais é igual a um:

log_a a = 1, pois a¹ = a

III) A potência de base “a” e expoente log_ab é igual a b:

a^{loga b}= b

IV) Dois logaritmos são iguais, numa mesma base, se os logaritmandos são iguais:

log_a b = log_a c

b = c

Propriedade dos logaritmos

1. Logaritmo do produto

O logaritmo do produto de dois fatores “a” e “b”, em qualquer base “c”, é igual à soma dos logaritmos de cada um desses fatores.

Se c > 0 e c ≠ 1, a > 0, b > 0, então:

log_c(a⋅b) = log_c a + log_c b

Exemplo:

log₃(9⋅27) = log₃9 + log₃27 = 2+3 =5

2. Logaritmo do quociente

O logaritmo do quociente de dois fatores a e b, em qualquer base c, é igual à diferença dos logaritmos de cada um desses fatores.

Se c > 0 e c ≠ 1, a > 0, b > 0, então:

log_c (a/b) = log_c a − log_c b

Exemplo:

log₃(27/9) = log₃ 27 − log₃ 9 = 3−2 = 1

3. Logaritmo da potência

O logaritmo de uma potência, em qualquer base c, é igual ao produto entre o expoente da potência e o logaritmo cujo logaritmando é a base da potência.

Se a > 0 e a ≠ 1, b > 0, c ∈ R, então:

log_a b^c = c * log_a b

Exemplo:

log₃ 9⁵ = 5 * log₃ 9 = 5 * 2 = 10

4. Logaritmo de uma raiz

O logaritmo da raiz enésima de um número real positivo é o produto entre o inverso do índice da raiz pelo logaritmo cujo o logaritmando é o radicando:

Se a > 0 e a≠1, b > 0, n∈N∗, então: