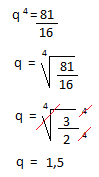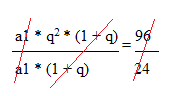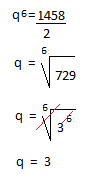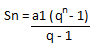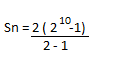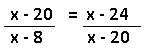.Respostas dos Exercícios – Progressão Aritmética e Geométrica

Juliana Jenny Kolb

Home > Concursos  > Questões de Concursos > Conhecimentos Gerais > Matemática e Raciocínio Lógico

Materiais de Estudo disponíveis

Apostila on-line

Respostas dos Exercícios – Progressão Aritmética e Geométrica

Resolução nr. 1: O próximo número da sequência -2, 6, -18, 54… é:

considerando os valores positivos, temos 6/2 = 3; 18/6 = 3, 54/18 = 3, então, encontramos a razão q=3, no caso, -3.

54 x -3 = -162

Resolução nr. 2: Qual é a soma de x, y e z para que a sequência 16, x, y, z, 81 seja uma progressão geométrica crescente?

Aplicando a fórmula: an = a1 * q^n-1

81 = 16 * q^5-1

Descobrindo os valores de x, y, z

16, x, y, z, 81

x = 16 * 1,5        x = 24

y = 24 * 1,5       y = 36

z = 36 * 1,5       z = 54

Somando x, y e z, temos: 114

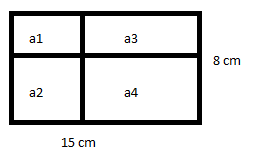
Resolução nr. 3: Um retângulo de 8cm de largura e 15cm de comprimento foi dividido em 4 regiões: a¹, a², a³ e a4 cujas áreas formam nesta ordem, uma progressão geométrica crescente. Se as somas das duas maiores áreas totaliza 96cm², qual é a diferença entre as áreas das duas menores regiões?

Área do retângulo = 15 * 8 = 120 cm²

Montando as equações:

a1 + a2 + a3 + a4 = 120

Sabemos que

a3 + a4 = 96     equação 1

Então,

a1 + a2 + 96 = 120

a1 + a2 = 24    equação 2

Modificando as equações em função de a1 (aplicando a fórmula: an = a1 * q^n-1):

• a2 = a1 * q^2-1
• a3 = a1 * q^3-1
• a4 = a1 * q^4-1

Equação 1:  (a1 * q^3-1 ) + ( a1 * q^4-1) = 96

• a1 * q²  + a1 * q³  =  96
• a1 * q²  * (1 + q) =  96

Equação 2:  (a1) + (  a1 * q^2-1 )  = 24

• a1 *  (1 + q) =  24

Dividindo membro a membro:

q² = 4

q = 2

Substituindo q = 2

a1 * (1 + 2) = 24

a1 = 8

Se a1 = 8 e q = 2

a2 = 16

A diferença entre as duas menores áreas é 8.

 

Resolução nr. 4:  Uma bactéria de determinada espécie divide-se em cada 2 horas. Depois de 24 horas, qual será o número total de bactérias.

Sequência (1, 2, 4, 8, …, an)

q = 2

Cuidado,  pegadinha: a divisão se dá de 2 em 2 horas, portanto, 12 intervalos. E em 12 intervalos, existirão 13 termos.

n = 13

Aplicando a fórmula: an = a1 * q^n-1

an = 1 * 2^13-1

an = 2¹²

an = 4096

 

Resolução nr. 5: Sobre o valor de x que torna as sequências x + 3, 3x + 1, 7x – 3 e 2x – 3, 2x + 4, 4x + 1 respectivamente, uma P.G e uma P.A., é correto afirmar que:

Precisamos descobrir o x.

A forma mais rápida é aplicar a propriedade da PA que diz que (a2 – a1) = (a3 – a2)

Então:

(2x + 4) – (2x -3) = (4x + 1) – (2x + 4)

x = 5   -> número primo

 

Resolução nr. 6: Durante os sete dias destinados às inscrições de um concurso, o número de candidatos cresceu em progressão geométrica do primeiro ao sétimo dia. Sabendo que no 1º dia se inscreveram 2 candidatos e no sétimo dia 1.458, concluímos que o total de candidatos inscritos para o referido concurso foi de:

a1 = 2

n = 7

an = 1458

Primeiro, precisamos descobrir a razão  (q).

Aplicando a fórmula: an = a1 * q^n-1

1458 = 2 * q^7-1

Agora, podemos calcular a soma, aplicando a fórmula:

Sn = 2186

 

Resolução nr. 7: O vazamento em um tanque de água provocou a perda de 2 litros de água no primeiro dia. Como o orifício responsável pela perda ia aumentando, no dia seguinte o vazamento foi o dobro do dia anterior. se essa perda perda foi dobrando a cada dia, o numero total de litros de água perdidos, até o 10º dia, foi de:

q = 2

n = 10

(2, 4, …. a10)

Aplicando a fórmula:

S10 = 2046

 

Resolução nr. 8: Os ângulos internos de um quadrilátero formam uma P.G. de modo que o ultimo ângulo é quadro vezes maior que o segundo ângulo. A medida do menor desses quatro ângulos, em graus, é:

Quadrilátero é um polígono convexo de 4 lados.

Sabemos que

*A soma dos ângulos internos de qualquer quadrilátero convexo é 360 graus.

a4 = 4 a2  equação 1

a1 + a2 + a3 + a4 = 360  equação 2

 

Modificando as equações em função de a1 (aplicando a fórmula: an = a1 * q^n-1):

• a2 = a1 * q^2-1
• a3 = a1 * q^3-1
• a4 = a1 * q^4-1

Equação 1:    a4 = 4 a2

• a1 * q³   = a1 * q^2-1
• q²= 4
• q = 2

Equação 2:  a1 + a2 + a3 + a4 = 360

• a1 + a1 * q¹  + a1 * q^3-1 + 4 a1 = 360
• …
• 15 a1 = 360
• a1 = 24

Como é uma PG crescente, a1 é o menor ângulo.

 

Resolução nr. 09:  Três números formam uma progressão aritmética de razão r=7 . Subtraindo-se uma unidade do primeiro termo, vinte unidades do segundo termo e trinta e uma unidades do terceiro termo, a sequência resultante é uma progressão geométrica de razão:

Aplicando as propriedade da PA: (x-r, x, x+r)

Sabemos que r = 7, então:

(x – 7, x, x + 7) aplicando as subtrações do enunciado, transformamos a equação em uma PG.

(x – 7 – 1, x – 20, x + 7 – 31)  =  (x – 8, x – 20, x – 24)

Aplicando as propriedade da PG: (a2 /a1) = (a3 / a2)

…

x = 26

Substituindo o x na equação:

(x – 8, x – 20, x – 24)

(18, 6, 2)

q = 1/3     …     (6/18) ou (2/6)

 

Resolução nr. 10: O número que deve ser somado aos termos da sequência (-2, 2, 14) para que esta se transforme numa progressão geométrica é:

Neste caso, é mais fácil utilizar as respostas para encontrar a solução.

Hipótese 1: (-2+5), (2+5), (14+5) = 3, 7, 19 -> não encontramos uma razão.

Hipótese 2: (-2+4), (2+4), (14+4) = 2, 6, 18 -> encontramos a razão q=3   -> (6/2=3), (18/6=3).

 

Resolução nr. 11: O financiamento de um carro foi feito nos seguintes moldes. Sem entrada e a primeira mensalidade de R$ 1,00, no segundo mês R$ 2,00, no terceiro mês R$ 4,00, e assim por diante até um total de 12 prestações. Qual é o custo final do carro.

(1, 2, 4, … an)

q = 2   (4/2 = 2, 2/1 = 2)

n = 12

Aplicando a fórmula:

…

S12 = 4095

Resolução nr. 12: Três pessoas se reuniram no dia 1º de janeiro de 2004 para iniciar uma ação de voluntariado junto a organizações de proteção ao meio ambiente. Em fevereiro, cada uma daquelas pessoas tinha conseguido a adesão de um novo voluntario. Observaram que tinham começado a aplicar uma boa estratégia para aumentar o grupo de voluntários e decidiram o seguinte: a cada mês, cada voluntário traria um novo voluntário para participar do grupo e, sempre que alguém desistisse, seria substituído. Assim, o total de voluntários no mês de janeiro de 2005, já incluídos os novos participantes do mês, será de:

Sabemos:

a1 = 3

n = 13 (meses)

q = 2

Aplicando a fórmula: an = a1 * q^n-1)

an = 3 * 2^13-1

an = 3 * 2¹²

 

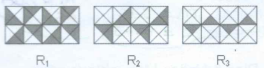
Resolução nr. 13:  Os retângulos R¹, R², e R³, representados na figura, são congruentes e estão divididos em regiões da mesma área. Ao se calcular o quociente entre a área da região pintada e a área total de cada um dos retângulos R¹, R², R³, verifica-se que os valores obtidos formam uma progressão geométrica (P.G.) decrescente de três termos. A razão dessa P.G. é:

Forma mais rápida/fácil:

Contando os triângulos escuros, temos:

16, 8, 4

q = 1/2  (8/16 = 1/2 e 4/8 = 1/2)

 

Resolução nr. 15:  Qual é a soma dos termos da sequência (x-2, 3x – 10, 10 + x, 5x + 2), para que a mesma seja uma progressão geométrica crescente?

 

14. Seja a sequencia (7 – x, x + 13, 45,…) uma progressão geométrica cresente. A soma dos dois primeiros termos dessa progressão é igual a:

 

 

20

18

16

22

17

15. Qual é a soma dos termos da sequência (x – 2, 3x – 10 x, 5x + 2), para que a mesma seja uma progressão geométrica crescente?

52

60

40

48

64