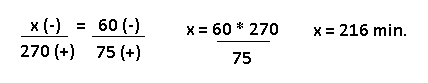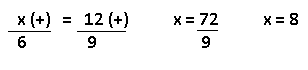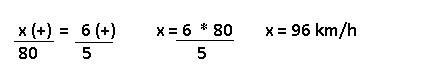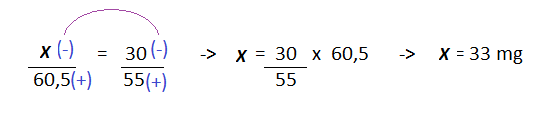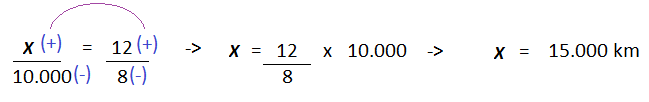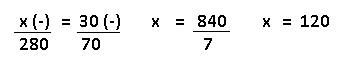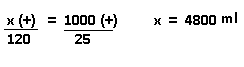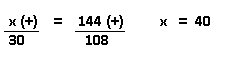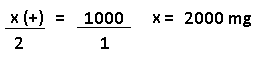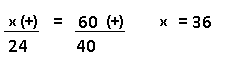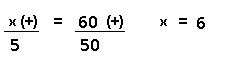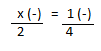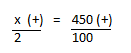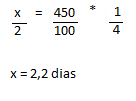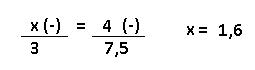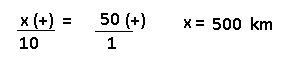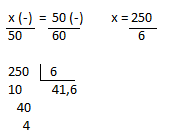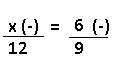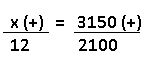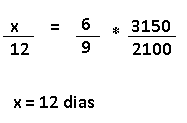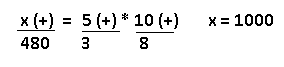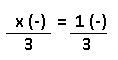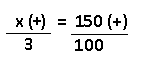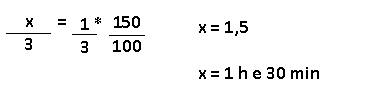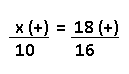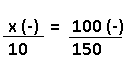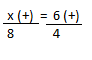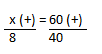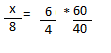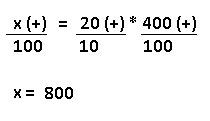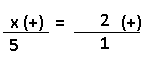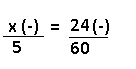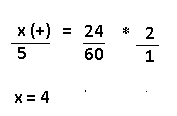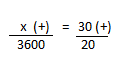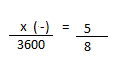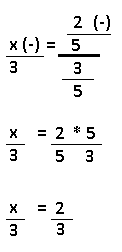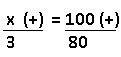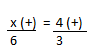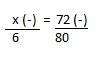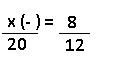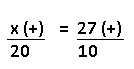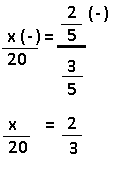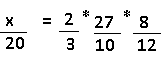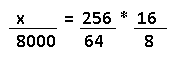Juliana Jenny Kolb
Home > Concursos > Questões de Concursos > Conhecimentos Gerais > Matemática e Raciocínio Lógico
Materiais de Estudo disponíveis
Respostas dos Exercícios – Regra de Três Simples e Composta
Resolução nr. 1: Se dirigir numa velocidade de 60 km/h um motorista faz um percurso em 270 minutos. Se a velocidade média fosse 15 km/h maior, o motorista faria o mesmo percurso em:
| 60 (-) -> é menor que 75 |
270 (+) |
| 75 (+) -> é maior que 60 |
x (-) -> se aumento a velocidade, diminuo o tempo |
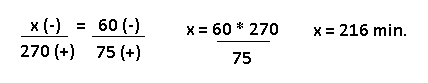
Resolução nr. 2: João mediu o lado de uma mesinha em palmos, obtendo, como resultado, exatos 3 palmos. Miguel foi “tirar a prova” e também mediu, usando a própria mão, obtendo exatos 4 palmos. Isso se explica pelo fato de Miguel ser filho de João e ter a mão menor. Tentando explicar ao filho o processo de medida, João transformou o próprio palmo em centímetros: 22 cm. Sabendo que ambos, pai e filho, medem em palmos usando os mesmos procedimentos (o que elimina erros de cálculo e aproximações), a medida da mão de Miguel é:
| 3 (-) -> menos palmos, mão de João |
22 (+) |
| 4 (+) -> mais palmos, mão de Miguel |
x (-) -> mão de Miguel é menor |

Ver: Sistemas de Medidas (+)
Resolução nr. 3: Para completar uma obra foram necessários 12 pedreiros trabalhando 6 horas por dia. Se a obra tivesse que ser feita com 3 pedreiros a menos então o total de horas necessárias para completar a obra seria de:
| 9 (-) -> menos 3 pedreiros |
x (+) -> Se menos pedreiros, mais tempo |
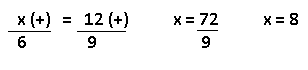
Resolução nr. 4: Um caminhão,viajando a uma velocidade média de 80 km/h, gasta 6 horas para percorrer um trajeto entre duas cidades. Qualé a velocidade média de um automóvel que percorre este mesmo trajeto em 5 horas?
| x (+) -> Se o tempo é menor, a velocidade é maior |
5 (-) -> tempo menor |
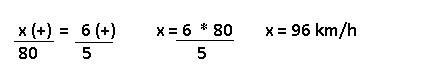
Resolução nr. 5: Se em cada porção de 55g de creme alimentício 60,5 mg são de cálcio, então o cálcio contido em 30 g desse creme é de:
| 30 (-) -> porção menor |
x (-) -> porção menor, menos cálcio |
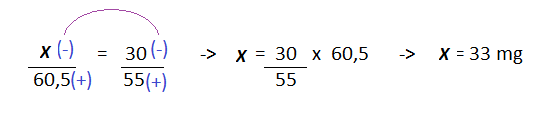
Resolução nr. 6: Durante 8 meses, Marcos rodou 10.000 km com seu carro. Se a proporção se mantiver, ao final de 12 meses ele terá rodado quantos quilômetros com seu carro?
| 12 (+) -> mais meses |
x (+) -> mais meses, maior quilometragem |
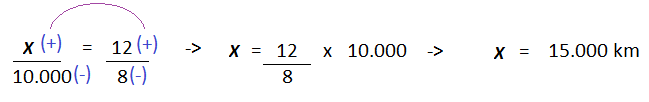
Resolução nr. 7: Uma fábrica possui, atualmente, 350 empregados, dos quais 20% são mulheres. Para aumentar a participação feminina nessa fábrica para 30% dos funcionários, sem demitir nenhum dos atuais empregados, quantas novas empregadas devem ser admitidas?
Primeiro, calcular a quantidade de homens e mulheres:
mulheres = 20/100 * 350 = 70.
Se 20% são mulheres, 80% são homens.
homens = 80/100 * 350 = 280.
| x (mulheres) (-) |
30 (aumentei para 30%) (-) |
| 280 (homens) (+) |
70 (diminuí para 70%) (+) |
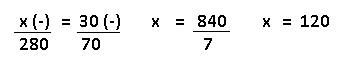
Se já existem 70 mulheres na fábrica, faltam 50 para chegar nos 120 (30%).
Resolução nr. 8: Correndo à velocidade constante de 12 km/h, quantos minutos são necessários para uma pessoa percorrer a distância de 3200 m?
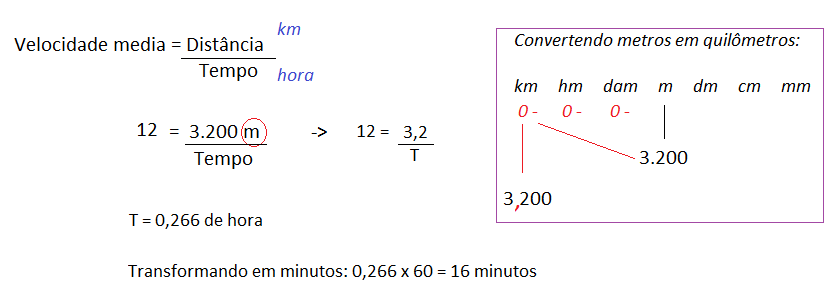
Ver: Sistemas de Medidas (+)
Resolução nr. 9: Sabendo-se que um copo de 120 ml de suco de laranja há 25 mg de vitamina C, quantos litros de suco de laranja são necessários para se obter 1 g de vitamina C?
Tenho as medidas em ml e mg, quero as mesmas em litros e gramas. Porém, para facilitar o cálculo, primeiro vamos converter 1 g em mg.
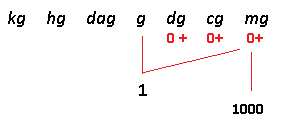
Então, 1 g = 1000 mg.
| x (+) |
1000 (+) se tenho mais mg, terei mais ml |
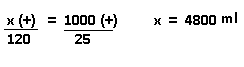
Convertendo ml em l:
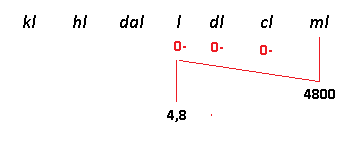
4,8 litros em 1 g de suco.
Ver: Sistemas de Medidas (+)
Resolução nr. 10. O Gerente do SAC (serviço de atendimento ao consumidor) de uma empresa constatou que 30 atendentes são capazes de atender satisfatoriamente, em média, 108 clientes por hora. Quantos funcionários são necessários para que o SAC desta empresa possa atender, em média, 144 clientes por hora, mantendo a mesma qualidade de atendimento?
| x (+) se tenho mais clientes/hora, terei mais atendentes |
144 (+) |
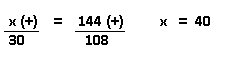
Resolução nr. 11: Uma empresa transportadora tem 180 encomendas para serem entregues em vários endereços da cidade. Observou-se que foram entregues 30 delas em 2 horas e 15 minutos. Se for mantida essa média de tempo gasto, para entregar todas as encomendas serão necessárias exatamente:
| 180 (+) mais encomendas, mais tempo |
x (+) |
| 30 (-) |
2 h 15 min = 135 mim (-) |

Ver: Sistemas de Medidas (+)
Resolução nr. 12: Se uma solução contém 2 mg/ml de uma substância dissolvida, quanto da substância existe em um litro da solução?
Converter l em ml: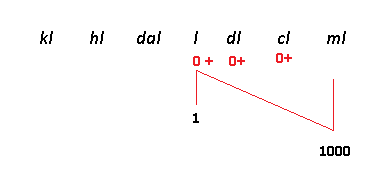
| x (+) mais ml, mais mg |
1 litro = 1000 ml (+) |
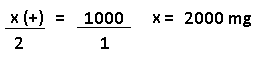
Convertendo mg em g:
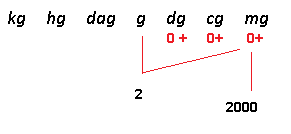
2 g de uma substância em 1 litro da solução.
Ver: Sistemas de Medidas (+)
Resolução nr. 13: Das 96 pessoas que participam de uma festa de confraternização dos funcionários do Departamento Nacional de Obras Contra as Secas, sabe-se que 75% eram do sexo masculino. Se, num dado momento antes do término da festa, foi constatado que a porcentagem dos homens havia se reduzido para 60% do total das pessoas presentes, enquanto que o número de mulheres permaneceu inalterado, até o final da festa, então a quantidade de homens que havia se retirado era
Início da festa => 96 pessoas
homens = 96 * 75/100 = 72
mulheres = (96 – 72) = 24
Final da festa => 60% homens, se diminui o % de homens, aumentou o de mulheres para 40% (100% – 60%).
| x homens (+) mais homens que mulheres |
60 (+) % maior de homens |
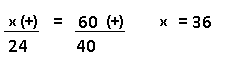
Resolução nr. 14: Um caminhão gasta 5 horas para fazer certo percurso a 60 km/h. Quanto tempo esse caminhão gastaria para fazer o mesmo percurso a uma velocidade de 50 km/h?
| 5 (-) |
60 (+) velocidade maior, menos tempo |
| x (+) |
50 (-) velocidade menor, mais tempo |
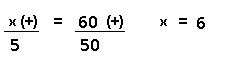
Resolução nr. 15: Um trajeto pode ser feito de automóvel, em uma hora e quarenta e cinco minutos, à velocidade média de 80 quilômetros por hora. Em quanto tempo se faz o mesmo trajeto à velocidade média de 70 quilômetros por hora?
| 1:45 (-) = (60 min + 45 min) = 105 min |
80 (+) velocidade maior, menos tempo |
| x (+) |
70 (-) velocidade menor, mais tempo |

Resolução nr. 16: Recentemente, a empresa Fast Brick Robotics mostrou ao mundo um robô, conhecido como Hadrian 105, capaz de construir casas em tempo recorde. Ele consegue trabalhar algo em torno de 20 vezes mais rápido que um ser humano, sendo capaz de construir até 150 casas por ano, segundo informações da empresa que o fabrica.
Tendo como referência as informações acima, julgue os itens a seguir.
Se um único robô constrói uma casa de 100 m2 em dois dias, então 4 robôs serão capazes de construir 6 casas de 75 m2 em menos de dois dias.
| Robôs |
Área Total |
Dias |
| 1 |
100 (1 casa * 100 m2) |
2 |
| 4 |
450 (6 casas * 75 m2) |
x |
Neste caso, analise os sinais separadamente:
| 4 (+) se eu tenho mais robôs, levarei menos tempo/dias |
x (-) |
Temos a relação:
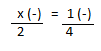
| 450 (+) se eu tenho mais área, levarei mais tempo/dias |
x (+) |
Temos a relação:
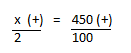
Montando a equação:
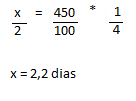
Resolução nr. 17: As instruções em uma lata de tinta dizem que 3 litros são suficientes para pintar uma área de 7,5 m2. Nessas condições, qual a quantidade de tinta necessária para pintar uma área de 4 m2?
| x (-) |
4 (-) área menor, quantidade de tinta (litros) menor |
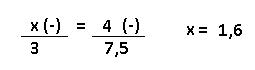
Resolução nr. 18: Um veículo cujo tanque tem capacidade de 50 litros consome 1 litro de combustível a cada 10 km rodados. Se o tanque do veículo estiver inicialmente cheio e este se mover à velocidade constante de 70 km/h, quanto tempo decorrerá, aproximadamente, até que o combustível acabe?
Sabemos que 1 litro de combustível, roda 10 km, vamos calcular quantos kms o veículo rodaria com o tanque cheio (50 litros).
| 50 (+) mais combustível, mais kms rodados |
x (+) |
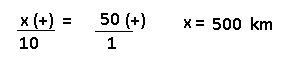
Sabemos que a velocidade é de 70 km/h (1 hora), e descobrimos que o tanque cheio faria 500 km, então:
| 500 (+) mais kms, mais tempo (horas) |
x (+) |
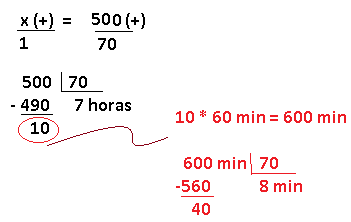
7 horas e 8 minutos, aproximadamente.
Resolução nr. 19: Para fiscalizar a segurança de certos dutos, um técnico de obras saiu da Companhia às 9h 20 mim e, mantendo a velocidade média de seu carro em 50 km/h, chegou ao local de vistoria às 10h 10 min. Se tivesse saído às 8h 30 min e tivesse feito o mesmo trajeto com a velocidade média de 60 km/h, teria chegado ao local da vistoria às
| Velocidade |
Tempo em minutos |
| 50 (-) |
50 (9:20 – 10:10) (+) |
| 60 (+) velocidade maior, menos tempo |
x (-) |
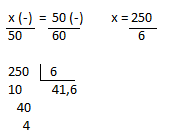
8:30 + 41,6 minutos = 9 h 11 min 40 s (aproximadamente)
Resolução nr. 20: Uma fábrica de brindes com 6 funcionários leva 12 dias para produzir 2100 unidades. Prevendo um aumento de vendas, o gerente decidiu contratar mais 3 funcionários. Nessas novas condições, quantos dias a fábrica levará para produzir 3150 unidades?
| Funcionários |
Dias |
Unidades |
| 6 |
12 |
2100 |
| 9 |
x |
3150 |
Neste caso, analise os sinais separadamente:
| 9 (+) se eu tenho mais funcionários, levarei menos tempo/dias |
x (-) |
Temos a relação:
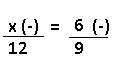
| x (+) |
3150 (+) mais unidades, mais dias |
Temos a relação:
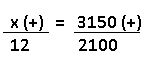
Montando a equação:
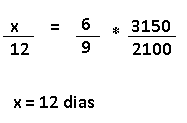
Resolução nr. 21: Numa clínica, três enfermeiras, trabalhando 8 horas por dia, atendem 480 pessoas. Com objetivo de aumentar o número de atendimentos, foram contratadas duas enfermeiras e a carga horária de trabalho de todas as enfermeiras passou a ser de 10 horas por dia. Pode-se esperar que o número de atendimentos passe a ser de:
| Qtde enfermeiras |
Horas |
Pessoas atendidas |
| 3 (-) |
8 (-) |
480 (-) |
| 3+2 = 5 (+) mais enfermeiras |
10 (+) mais horas |
x (+) espera-se mais atendimentos |
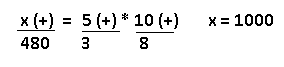
Resolução nr. 22: Numa secretaria, 10 pessoas, trabalhando com o mesmo ritmo e cada um em seu PC, durante 10 dias, com 8 horas de trabalho diário digitam 650 boletins de notas. quantas pessoas, nas mesmas condições, serão necessárias para digitar 1300 boletins em 8 dias, trabalhando 4 horas por dia?
| Pessoas |
Dias * Horas |
Boletins |
| 10 (-) |
10 * 8 = 80 (+) |
650 (-) |
| x (+) mais pessoas, pois temos menos horas e mais boletins |
8 * 4 = 32 (-) menos horas |
1300 (+) mais boletins |

Resolução nr. 23: Uma impressora trabalhando continuamente emite todos os boletos de pagamento de uma empresa em 3 horas. Havendo um aumento de 50% no total de boletos a serem emitidos, três impressoras, iguais à primeira, trabalhando juntas poderão realizar o trabalho em 1 hora e:
Primeiro, como não existem valores atribuídos aos “boletos”, crie valores para poder dar continuidade. Exemplo: 100 e 150 ( 100 + 50% = 150)
| Impressoras |
Horas |
Boletos |
| 1 |
3 |
100 |
| 3 |
x |
150 |
Neste caso, analise os sinais separadamente:
| 3 (+) mais impressoras, menos horas |
x (-) |
Temos a relação:
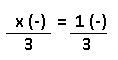
| x (+) |
150 (+) mais boletos, mais horas |
Temos a relação:
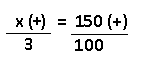
Montando a equação:
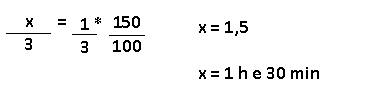
Resolução nr. 24: Uma indústria tem 34 máquinas. Sabe-se que 18 dessas máquinas têm, todas, a mesma eficiência e executam certo serviço em 10 horas de funcionamento contínuo. Se as máquinas restantes têm 50 % a mais de eficiência que as primeiras, funcionando ininterruptamente, executariam o mesmo serviço em:
Primeiro, como não existem valores atribuídos em “eficiência”, crie valores para poder dar continuidade. Exemplo: 100 e 150 ( 100 + 50% = 150)
| Máquinas |
Horas |
Eficiência |
| 18 |
10 |
100 |
| 16 |
x |
150 |
Neste caso, analise os sinais separadamente:
| 16 (-) menos máquinas, mais horas |
x (+) |
Temos a relação:
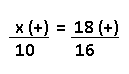
| x (-) |
150 (+) mais eficiência, menos horas |
Temos a relação:
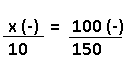
Montando a equação:
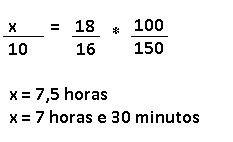
Resolução nr. 25: Oito trabalhadores, trabalhando com desempenhos constantes e iguais, são contratados para realizar uma tarefa no prazo estabelecido de 10 dias. Decorridos 6 dias, como apenas 40% da tarefa havia sido concluída, decidiu-se contratar mais trabalhadores a partir do sétimo dia, com as mesmas características dos anteriores, para concluir a tarefa no prazo inicialmente estabelecido. A quantidade de trabalhadores contratados a mais, a partir do sétimo dia, foi de
| Trabalhadores |
Dias |
% |
| 8 |
6 |
40/100 * 100 |
| x |
4 |
60/100 * 100 |
Neste caso, analise os sinais separadamente:
| x (+) terei mais trabalhadores (contratados) |
4 (-) menos dias |
Temos a relação:
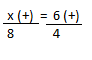
| x (+) terei mais trabalhadores (contratados) |
60 (+) maior percentual |
Temos a relação:
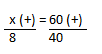
Montando a equação:
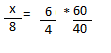
x = 18 trabalhadores no total.
10 trabalhadores a mais (contratados).
Resolução nr. 26: Sabe-se que 10 máquinas, todas com a mesma capacidade operacional, são capazes de montar 100 aparelhos em 10 dias, se funcionarem ininterruptamente 10 horas por dia. Nessas condições, o número de aparelhos que poderiam ser montados por 20 daquelas máquinas, em 20 dias de trabalho e 20 horas por dia de funcionamento ininterrupto, é
| Máquinas |
Aparelhos |
Dias x Horas |
| 10 (-) |
100 (-) |
10 * 10 = 100 horas (-) |
| 20 (+) Se mais máquinas e mais horas, mais aparelhos |
x (+) |
20 * 20 = 400 horas (+) |
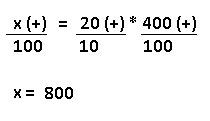
Resolução nr. 27: Cinco máquinas idênticas, trabalhando 8 horas por dia, levam 3 dias para produzir certa quantidade de peças. Quantas dessas máquinas, trabalhando 12 horas por dia, durante 5 dias, serão necessárias para produzir o dobro dessa quantidade de peças?
Primeiro, como não existem valores atribuídos para “aparelhos”, crie valores para poder dar continuidade. Exemplo: 1 e 2 ( dobro)
| Máquinas |
Aparelhos |
Dias x Horas |
| 5 |
1 |
3 * 8 = 24 |
| x |
2 |
5 * 12 = 60 |
Neste caso, analise os sinais separadamente:
| x (+) |
2 (+) mais aparelhos, necessitam de mais máquinas |
Temos a relação:
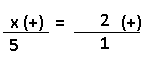
| 5 (+) |
24 (-) Se menos tempo, mais máquinas |
Temos a relação:
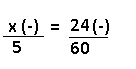
Montando a equação:
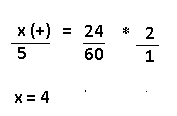
Resolução nr. 28: Um supermercado dispõe de 20 atendentes que trabalham 8 horas por dia e custam R$ 3.600,00 por mês. Se o supermercado passar a ter 30 atendentes trabalhando 5 horas por dia, eles custarão, por mês,
| Atendentes |
Horas |
R$ |
| 20 |
8 |
3600 |
| 30 |
5 |
x |
Neste caso, analise os sinais separadamente:
| 30 (+) Se tenho mais atendentes, tenho um custo maior |
x (+) |
Temos a relação:
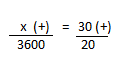
| 5 (-) menos horas, menor custo |
x (-) |
Temos a relação:
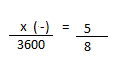
Montando a equação:
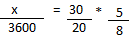
x = R$ 3375,00
Resolução nr. 29: Hoje, Filomena gastou 3 horas de trabalho ininterrupto para digitar 3/5 do total de páginas de um texto e, amanhã, Gertrudes deverá digitar as páginas restantes. Considerando que a capacidade operacional de Gertrudes é 80% da capacidade de Filomena, então, o esperado é que Gertrudes digite a sua parte em
| Horas |
Páginas |
Eficiência % |
| 3 |
3/5 |
100 |
| x |
2/5 |
80 |
Neste caso, analise os sinais separadamente:
| 3 (+) mais horas |
3/5 (+) mais páginas |
| x (-) menos horas |
2/5 (-) menos páginas |
Temos a relação:
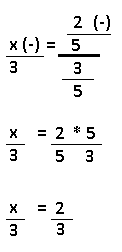
| x (+) |
80 (-) menos eficiência, mais horas |
Temos a relação:
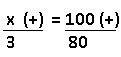
Montando a equação:

Resolução nr. 30: Três equipes trabalham na recuperação de uma estrada e terminaram de fazer 6 km em 10 dias, com 8 horas de trabalho por dia. Se, em outro trecho, 4 equipes com a mesma produtividade das anteriores trabalharem 6 horas por dia, durante 12 dias, recuperarão:
| Equipes |
km |
Horas |
| 3 |
6 |
10 * 8 = 80 |
| 4 |
x |
12 * 6 = 72 |
Neste caso, analise os sinais separadamente:
| 4 (+) Se tenho mais equipes, faço mais kms |
x (+) |
Temos a relação:
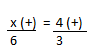
| x (-) menos horas, menos kms |
72 (-) |
Temos a relação:
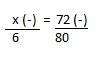
Montando a equação:

Resolução nr. 31: Sabendo que 20 costureiras, trabalhando 8 horas por dia, conseguiram aprontar 3/5 de uma encomenda em 27 dias, quantas costureiras a mais serão necessárias para concluir essa tarefa em 10 dias, sendo que todas as costureiras (antigas e novas) passarão a trabalhar 12 horas por dia?
| costureiras |
horas – dias |
tarefa |
| 20 |
8 27 |
3/5 |
| x |
12 10 |
2/5 |
Neste caso, analise os sinais separadamente, inclusive as horas e dias:
| x (-) |
12 (+) mais horas, menos costureiras |
Temos a relação:
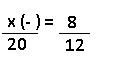
Temos a relação:
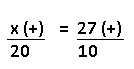
| x (-) |
2/5 (-) menos qtde de tarefa |
Temos a relação:
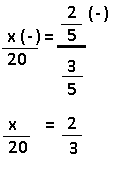
Montando a equação:
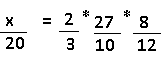
x = 24 costureiras
A mais -> 24 – 20 = 4
Resolução nr. 32: Suponha que 8 máquinas de terraplanagem, todas com a mesma capacidade operacional, sejam capazes de nivelar uma superfície de 8.000 metros quadrados em 8 dias, se funcionarem ininterruptamente 8 horas por dia. Nas mesmas condições, quantos metros quadrados poderiam ser nivelados por 16 daquelas máquinas, em 16 dias de trabalho e 16 horas por dia de funcionamento ininterrupto?
| máquinas |
m2 |
dias horas |
| 8 (-) menos máquinas |
8000 (menos metros) |
8 * 8 = 64 (-) |
| 16 (+) mais máquinas |
x (+) |
16 * 16 = 256 (+) |
Neste caso, podemos fazer a análise direta dos sinais:
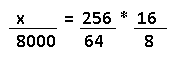
x = 64.000