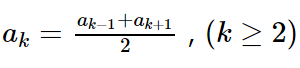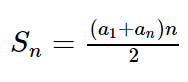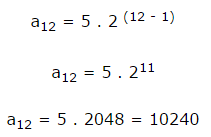Juliana Jenny Kolb
Home > Concursos > Questões de Concursos > Conhecimentos Gerais > Matemática e Raciocínio Lógico
Progressão Aritmética e Geométrica
Progressão Aritmética
Definimos Progressão Aritmética (PA) como sendo uma sequência numérica em que cada termo, a partir do segundo, é igual a soma do termo anterior com uma constante. Na P.A temos a presença de uma constante chamada de razão (r), sendo a mesma obtida por meio da diferença de um termo da sequência pelo seu anterior. Confira alguns exemplos:
A razão da P.A é representada por r = 4 – 1 = 3
A sequência (1, 6, 11, 16, 21…) é uma PA.
A razão da P.A é representada por r = 6 – 1 = 5
Classificação das Progressões aritméticas
As progressões aritméticas podem ser classificadas em: crescente, decrescente e constante.
Crescente: Para que uma P.A seja crescente a sua razão (r) deve ser positiva, ou seja, r > 0. A sequência numérica será crescente quando, cada termo a partir do segundo for maior que o antecessor. Exemplo: (1, 3, 5, 7, …) é uma PA crescente de razão 2.
Decrescente: Uma PA será decrescente se a sua razão (r) for negativa, ou seja, r < 0. A sequência numérica será decrescente quando, cada termo a partir do segundo for menor que o antecessor. Exemplo: (15, 10, 5, 0, -5 …) é uma PA decrescente de razão – 5.
Constante: Para uma PA ser constante a sua razão deve ser nula, ou seja, r = 0. Todos os seus termos serão iguais. Exemplo: (2, 2, 2, …) é uma PA constante de razão nula.
Fórmula do termo geral de uma Progressão aritmética
Quando partimos do primeiro termo da sequência, a fórmula do termo geral de uma P.A (a1, a2, a3, …,, an, …) de razão r é representada por:
an=a1+(n−1)⋅r
- an = Termo geral
- a1 = Primeiro termo da sequência.
- n = Número de termos da P.A. ou posição do termo numérico na P.A
- r = Razão
Exemplo:
Determine o 20º termo da P.A. (2, 4, 6, 8 …)
Dados da questão: a1 = 2, r = 2, n = 20, a20 = ?
an=a1+(n−1)⋅r
a20=2+(20−1)⋅2
a20=2+(19)⋅2
a20=2+38=40
O vigésimo termo da P.A. é 40.
Propriedades de uma PA
Em uma PA qualquer, de n termos e razão r, podemos observar as seguintes propriedades:
→ Qualquer termo de uma PA, a partir do segundo, é a média aritmética entre o anterior e o posterior.
Soma dos termos de uma PA finita
É dada pela fórmula:
Progressão Geométrica
As Progressões Geométricas (PG) são formadas por uma sequência numérica, em que estes números são definidos (exceto o primeiro) utilizando a constante q, chamada de razão. O próximo número da P.G. é o número atual multiplicado por q. Exemplo:
(1, 2, 4, 8, 16, 32, 64, 128, 256, 512, …), a razão é 2
A razão pode ser qualquer número racional (positivos, negativos, frações, exceto o zero). Para descobrir qual a razão de uma PG, basta escolher qualquer número da sequência, e dividir pelo número anterior.
Fórmula do termo geral
A sequinte fórmula pode ser utilizada para encontrar qualquer valor de uma sequência em progressão geométrica:
em que a é um termo, então a1 refere-se ao primeiro termo. No lugar de n colocamos o número do termo que queremos encontrar. Exemplo:
q = 2
a1 = 5
para descobrir, por exemplo, o termo a12, faremos:
Classificação das Progressões Geométricas
Oscilante
Neste tipo de PG, a razão é negativa, o que fará com que a sequência numérica seja composta de números negativos e positivos, se intercalando.
(3, -6, 12, -24, 48, -96, 192, -384, 768,…), em que a razão é -2
Crescente
Uma PG é considerada crescente quando q > 1 e a1 > 0, ou quando 0 < q < 1 e a1 < 0:
(1, 3, 9, 27, 81, …), onde a razão é 3 e a1 > 0 (primeiro caso)
(-4, -2, -1, -0,5, -0,25, -0,125 …), onde a razão é 0,5 e a1 < 0 (segundo caso)
Constante
Nesta PG, a sequência numérica tem sempre os mesmos números. Para isso, a razão deve ser sempre 1:
(4, 4, 4, 4, 4, 4, 4, …) onde a razão é 1
Decrescente
Uma PG é considerada decrescente quando q > 1 e a1 < 0, ou quando 0 < q < 1 e a1 > 0. Assim, os números da sequência são sempre menores do que o número anterior:
(-4, -8, -16, -32 …), razão = 2 (primeiro caso)
(64, 32, 16, 8, 4, 2, 1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, ..) razão = 1/2 (segundo caso)
Site de Referência
http://www.infoescola.com/