Juliana Jenny Kolb
Home > Concursos > Questões de Concursos > Conhecimentos Gerais > Matemática e Raciocínio Lógico > Questões Matemática e Raciocínio Lógico
Materiais de Estudo disponíveis
| Exercícios Resolvidos |  |
Teste 1: Matemática e Raciocínio Lógico
Questões extraídas de concursos públicos e/ou provas de certificação. Cada teste apresenta no máximo 30 questões.
Resolução nr 41 da página Respostas dos Exercícios – Estruturas Lógicas, Proposições simples e compostas – Resolução nr 36 da página Respostas dos Exercícios – Estruturas Lógicas, Proposições simples e compostas – Resolução nr 39 da página Respostas dos Exercícios – Estruturas Lógicas, Proposições simples e compostas – Resolução nr 37 da página Respostas dos Exercícios – Estruturas Lógicas, Proposições simples e compostas – Resolução nr 38 da página Respostas dos Exercícios – Estruturas Lógicas, Proposições simples e compostas –Results
#1. (VUNESP – TCE-SP/2015) Procurando encontrar o tom exato da cor solicitada pelo cliente, um pintor preparou uma mistura de três tintas, A, B e C. Usou certa lata como medida e misturou, em um balde, 3/5 de lata de tinta A, 2/3 de lata de tinta B e 4/3 de lata de tinta C. Da mistura preparada, reservou uma quantidade equivalente a duas latas (medida) completamente cheias e usou totalmente o restante para pintar uma área de 6,3 m², como teste. Desse modo, é correto afirmar que, aplicada de forma idêntica à aplicada na área teste, cada lata (medida) dessa mistura permite pintar uma área igual, em m², a
#2. (VUNESP – TCE-SP/2015) O responsável pela expedição constatou que o número de caixas de um lote de certo produto era 50% maior que o número máximo de caixas que poderiam ser carregadas no veículo designado para o transporte. Providenciou, então, um segundo veículo, idêntico ao primeiro, dividiu as caixas desse lote em dois grupos de igual número, sem restar nenhuma, e colocou cada grupo de caixas em um dos veículos. Se após o carregamento restou espaço para mais 12 dessas caixas em cada veículo, então é correto afirmar que o número total de caixas carregadas nos dois veículos foi igual a
#3. (VUNESP – TCE-SP/2015) Em um terreno retangular, cuja medida do perímetro é igual a P, a razão entre as medidas de comprimento (C) e largura (L), nessa ordem, é 5/2. Desse modo, é correto afirmar que
#4. (VUNESP – TCE-SP/2015) Para certo ambulante, o lucro (L) é dado pela diferença entre o preço de venda (PV) e o preço de compra (PC) de cada produto vendido. Se o lucro obtido em certo produto é igual a 60% do seu preço de venda, então o preço de venda desse produto é igual ao seu preço de custo aumentado em
#5. (VUNESP – TCE-SP/2015) Uma equivalente para a afirmação “Se Carlos foi aprovado no concurso, então ele estudou” está contida na alternativa:
?
Questão resolvida, nr 41 da página de respostas
#6. (VUNESP – TCE-SP/2015) Se Reginaldo é agente da fiscalização ou Sérgio é professor, então Márcia é psicóloga. André é administrador se, e somente se, Carmem é dentista. Constatado que Márcia não é psicóloga e André não é administrador, conclui-se corretamente que
?
Questão resolvida, nr 36 da página de respostas
#7. (VUNESP – TCE-SP/2015) Sabe-se que todos os primos de Vanderlei são funcionários públicos e que todos os primos de Marcelo não são funcionários públicos. Dessa forma, deduz-se corretamente que
#8. (VUNESP – TCE-SP/2015) Sabe-se que Débora é 5 centímetros mais baixa que Antonio e 4 centímetros mais alta que Mirian. Sabe-se, também, que Eduardo é 3 centímetros mais alto que Antonio e 12 centímetros mais alto que Carlos. Se for verdadeiro que Carlos é 10 centímetros mais alto que Wilson, que mede 1,65 metro, então é correto afirmar que a altura de Antonio, em metro, será
#9. (FCC – DPE-SP/2013) A figura abaixo possui 12 círculos dispostos em quatro filas de quatro círculos.
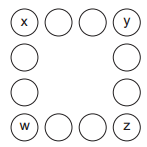Os círculos devem ser preenchidos com números naturais de 1 a 12, sem repetição, e de forma que a soma dos números em cada uma das quatro filas seja sempre 22. Atendendo à essas condições, a soma dos números colocados nos círculos indicados por x, y, z e w será #10. (FCC – DPE-SP/2013)
#11. (CESPE – SERPRO/2013) Ser síndico não é fácil. Além das cobranças de uns e da inadimplência de outros, ele está sujeito a passar por desonesto. A esse respeito, um ex-síndico formulou as seguintes proposições: — Se o síndico troca de carro ou reforma seu apartamento, dizem que ele usou dinheiro do condomínio em benefício próprio. (P1) — Se dizem que o síndico usou dinheiro do condomínio em benefício próprio, ele fica com fama de desonesto. (P2) — Logo, se você quiser manter sua fama de honesto, não queira ser síndico. (P3) Com referência às proposições P1 , P2 e P3 acima, julgue: Considerando que P1 e P2 sejam as premissas de um argumento de que P3 seja a conclusão, é correto afirmar que, do ponto de vista lógico, o texto acima constitui um argumento válido.
#12. (CESPE – SERPRO/2013) Ser síndico não é fácil. Além das cobranças de uns e da inadimplência de outros, ele está sujeito a passar por desonesto. A esse respeito, um ex-síndico formulou as seguintes proposições: — Se o síndico troca de carro ou reforma seu apartamento, dizem que ele usou dinheiro do condomínio em benefício próprio. (P1) — Se dizem que o síndico usou dinheiro do condomínio em benefício próprio, ele fica com fama de desonesto. (P2) — Logo, se você quiser manter sua fama de honesto, não queira ser síndico. (P3) Com referência às proposições P1 , P2 e P3 acima, julgue: A negação da proposição “O síndico troca de carro ou reforma seu apartamento” pode ser corretamente expressa por “O síndico não troca de carro nem reforma seu apartamento”.
#13. (CESPE – SERPRO/2013) Ser síndico não é fácil. Além das cobranças de uns e da inadimplência de outros, ele está sujeito a passar por desonesto. A esse respeito, um ex-síndico formulou as seguintes proposições: — Se o síndico troca de carro ou reforma seu apartamento, dizem que ele usou dinheiro do condomínio em benefício próprio. (P1) — Se dizem que o síndico usou dinheiro do condomínio em benefício próprio, ele fica com fama de desonesto. (P2) — Logo, se você quiser manter sua fama de honesto, não queira ser síndico. (P3) Com referência às proposições P1 , P2 e P3 acima, julgue: A partir das premissas P1 e P2 , é correto concluir que a proposição “Se o síndico ficou com fama de desonesto, então ele trocou de carro” é verdadeira.
?
Questão resolvida, nr 39 da página de respostas
#14. (CESPE – SERPRO/2013) Ser síndico não é fácil. Além das cobranças de uns e da inadimplência de outros, ele está sujeito a passar por desonesto. A esse respeito, um ex-síndico formulou as seguintes proposições: — Se o síndico troca de carro ou reforma seu apartamento, dizem que ele usou dinheiro do condomínio em benefício próprio. (P1) — Se dizem que o síndico usou dinheiro do condomínio em benefício próprio, ele fica com fama de desonesto. (P2) — Logo, se você quiser manter sua fama de honesto, não queira ser síndico. (P3) Com referência às proposições P1 , P2 e P3 acima, julgue: Se a proposição “Dizem que o síndico usou dinheiro do condomínio em benefício próprio” for falsa, então, independentemente do valor lógico da proposição “O síndico fica com fama de desonesto”, a premissa P2 será verdadeira.
?
Questão resolvida, nr 37 da página de respostas
#15. (CESPE – SERPRO/2013) Estudos revelam que 95% dos erros de digitação de uma sequência numérica — como, por exemplo, um código de barras ou uma senha — são a substituição de um algarismo por outro ou a troca entre dois algarismos da mesma sequência; esse último tipo de erro corresponde a 80% dos casos. Considerando esses fatos e que a senha de acesso de um usuário a seu provedor de email seja formada por 8 algarismos, escolhidos entre os algarismos de 0 a 9, julgue: Infere-se das informações que a probabilidade de ocorrer um erro de troca entre dois algarismos da própria sequência no momento da digitação de uma sequência numérica é de 80%.
#16. (CESPE – SERPRO/2013) Estudos revelam que 95% dos erros de digitação de uma sequência numérica — como, por exemplo, um código de barras ou uma senha — são a substituição de um algarismo por outro ou a troca entre dois algarismos da mesma sequência; esse último tipo de erro corresponde a 80% dos casos. Considerando esses fatos e que a senha de acesso de um usuário a seu provedor de email seja formada por 8 algarismos, escolhidos entre os algarismos de 0 a 9, julgue: Se, ao digitar a sua senha, o usuário cometer um erro do tipo substituição de um algarismo por outro, então a probabilidade de que tal substituição ocorria no primeiro algarismo da senha será igual a 0,1.
#17. (CESPE – SERPRO/2013) Estudos revelam que 95% dos erros de digitação de uma sequência numérica — como, por exemplo, um código de barras ou uma senha — são a substituição de um algarismo por outro ou a troca entre dois algarismos da mesma sequência; esse último tipo de erro corresponde a 80% dos casos. Considerando esses fatos e que a senha de acesso de um usuário a seu provedor de email seja formada por 8 algarismos, escolhidos entre os algarismos de 0 a 9, julgue: A quantidade de maneiras distintas de o usuário, ao digitar a sua senha, cometer um erro do tipo troca entre dois algarismos da própria sequência é superior a 30.
#18. (UNICENTRO – UNICENTRO/2016)
#19. (UNICENTRO – UNICENTRO/2016) Considere uma progressão aritmética (P.A.) cujo terceiro termo é 2 e o oitavo termo é 17. Assinale a alternativa que representa a soma dos dois primeiros termos dessa P.A.:
#20. (UNICENTRO – UNICENTRO/2016)
#21. (UNICENTRO – UNICENTRO/2016) Considere verdadeiras as seguintes afirmações: I. Todos os candidatos são esforçados. II. Existem candidatos que concluíram curso de pós-graduação. Baseando-se nessas afirmativas, conclui-se que
#22. (UNICENTRO – UNICENTRO/2016) Para calcular a altura de um prédio, um engenheiro utilizou a seguinte metodologia. No mesmo instante, mediu a sua própria sombra e a sombra projetada pelo prédio obtendo, respectivamente, 40 cm e 1,2 m. Sabendo que a altura do engenheiro é de 1,7 m, qual é a altura do prédio?
#23. (UNICENTRO – UNICENTRO/2016) Dos 60 alunos de uma classe, 25 foram aprovados em Matemática, 35 foram aprovados em Português, 36 foram aprovados em Geografia, 10 em Geografia e Matemática, 18 em Português e Matemática, 19 em Português e Geografia e somente 5 alunos foram aprovados nas três disciplinas. Quantos alunos não foram aprovados em nenhuma das três disciplinas?
#24. (UNICENTRO – UNICENTRO/2016) O gasto de João com a mensalidade da escola de seus filhos correspondia a 20% do seu salário no ano de 2015. Em janeiro de 2016, João teve um reajuste salarial de 4%, porém a mensalidade da escola teve um reajuste de 30%. Desse modo, qual é a porcentagem do salário de João destinada ao pagamento da mensalidade escolar atualmente?
#25. (UNICENTRO – UNICENTRO/2016) O número de vagas disponibilizadas por determinada escola segue a função dada por f (n) = 40 n + 100 na qual n é um número natural e representa o número de anos desde a fundação. Nessa mesma escola, o número de alunos matriculados anualmente segue a função dada por g (n) = 2 n² + 30 n + 100. Dessa maneira, quantos anos, após a fundação, o número de alunos matriculados anualmente atingirá o número de vagas disponibilizadas pela escola?
#26. (UEL/COPS – UEL/2015) Leia a afirmação a seguir. Se eu caso então eu compro uma bicicleta. Assinale a alternativa que apresenta, corretamente, uma sentença logicamente equivalente a essa afirmação.
?
Questão resolvida, nr 38 da página de respostas
#27. (UEL/COPS – UEL/2015) Dr. K. Vera está para receber sua sentença de morte. Seus algozes o desafiam: Faça uma afirmação qualquer. Se você falar a verdade, será afogado. Se o que disser for falso, morrerá enforcado. Entretanto, se não pudermos definir sua afirmação como verdadeira ou falsa, será poupado e libertado. Nessas condições e considerando os princípios da argumentação lógica, assinale a alternativa que apresenta, corretamente, uma afirmação que o Dr. K. Vera pode dizer para se salvar da sentença de morte.
#28. (UEL/COPS – UEL/2015) Leia a proposição P a seguir, que é uma paráfrase de um verso de Fernando Pessoa. Se a alma não é pequena então tudo vale a pena. Em relação à proposição P, considere as afirmativas a seguir. I. Uma proposição logicamente equivalente a P é dada por: A alma é pequena ou nada vale a pena. II. A negação lógica da proposição P é dada por: Se a alma é pequena então nada vale a pena. III. A contrapositiva da proposição P é dada por: Se algo vale a pena então a alma é pequena. IV. A recíproca da proposição P é dada por: Se tudo vale a pena então a alma não é pequena. Assinale a alternativa correta.
#29. (UEL/COPS – UEL/2015) Maria é formada em Direito e deseja fazer alguns cursos de especialização. A probabilidade de matricular-se em uma especialização em Direito Criminal é de 0,38, a probabilidade de matricular-se em um curso de Direito Civil é de 0,21 e a probabilidade de matricular-se em ambos os cursos é de 0,05. A partir dessas informações, assinale a alternativa que apresenta, corretamente, a probabilidade de Maria não se matricular em qualquer uma dessas duas especializações.
#30. (UNICENTRO – UNICENTRO/2016) Uma bibliotecária precisa organizar um conjunto de livros em uma estante. Esse conjunto é composto por três livros de Química, quatro livros de Matemática e dois livros de Física. De quantas maneiras diferentes esses livros poderão ser organizados, sendo que os livros de uma mesma disciplina não poderão ficar separados e o grupo de livros de Física deverá estar sempre entre os livros de Química e Matemática?
